尝试数形结合解释投影矩阵
某天忽然想到了一种可能更易理解投影矩阵的方法,所以有了本文。
目录
MVP 变换
我们知道,要把一个三维的顶点坐标映射到二维的屏幕上,需要将顶点坐标依次经过 model matrix、view matrix 和 projection matrix 变换,得到 clip space 下的坐标,这个过程简称为 MVP 变换。然后将 clip space 坐标除以自身的 w 分量,得到 NDC(normalized device coordinates)坐标,而图形 API 内部会自动地除以 w 分量,所以不需要我们手动处理(只需把 clip space 的坐标传给gl_Position即可)。最后图形 API 再将 viewport matrix 应用到 DNC,得到屏幕坐标。
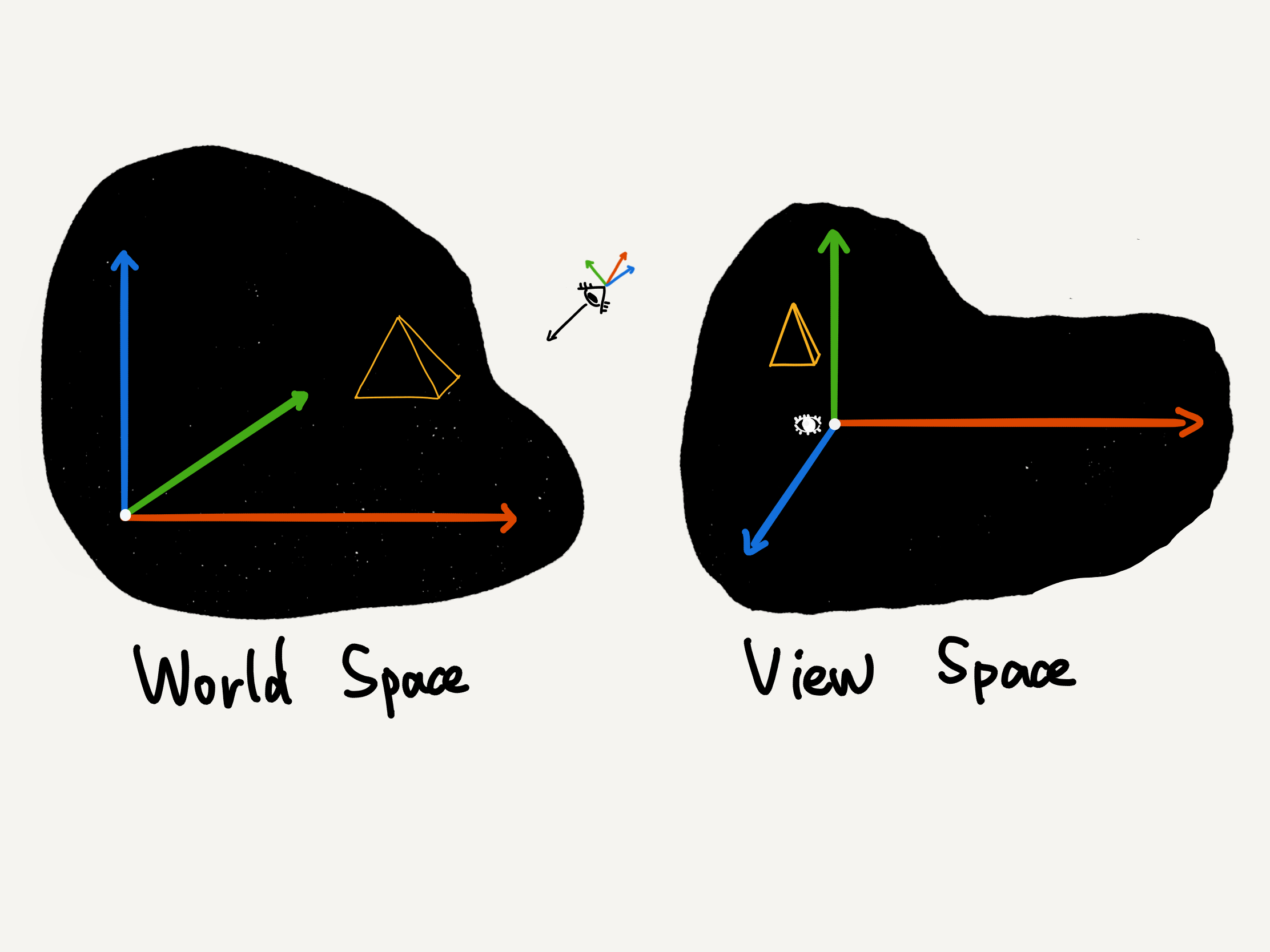
当处于世界坐标系的顶点坐标经过 view matrix 变换后,所处的坐标系就变成了这样的:
- 以相机的 position 作为坐标系的原点
- 以相机的 direction 作为坐标系的 -Z 轴
- 以相机的 right 作为坐标系的 X 轴和
- 以相机的 up 作为坐标系 Y 轴
该坐标系对应的矩阵称为 camera matrix,它与 view matrix 互逆,该坐标系即为 view space。
投影矩阵
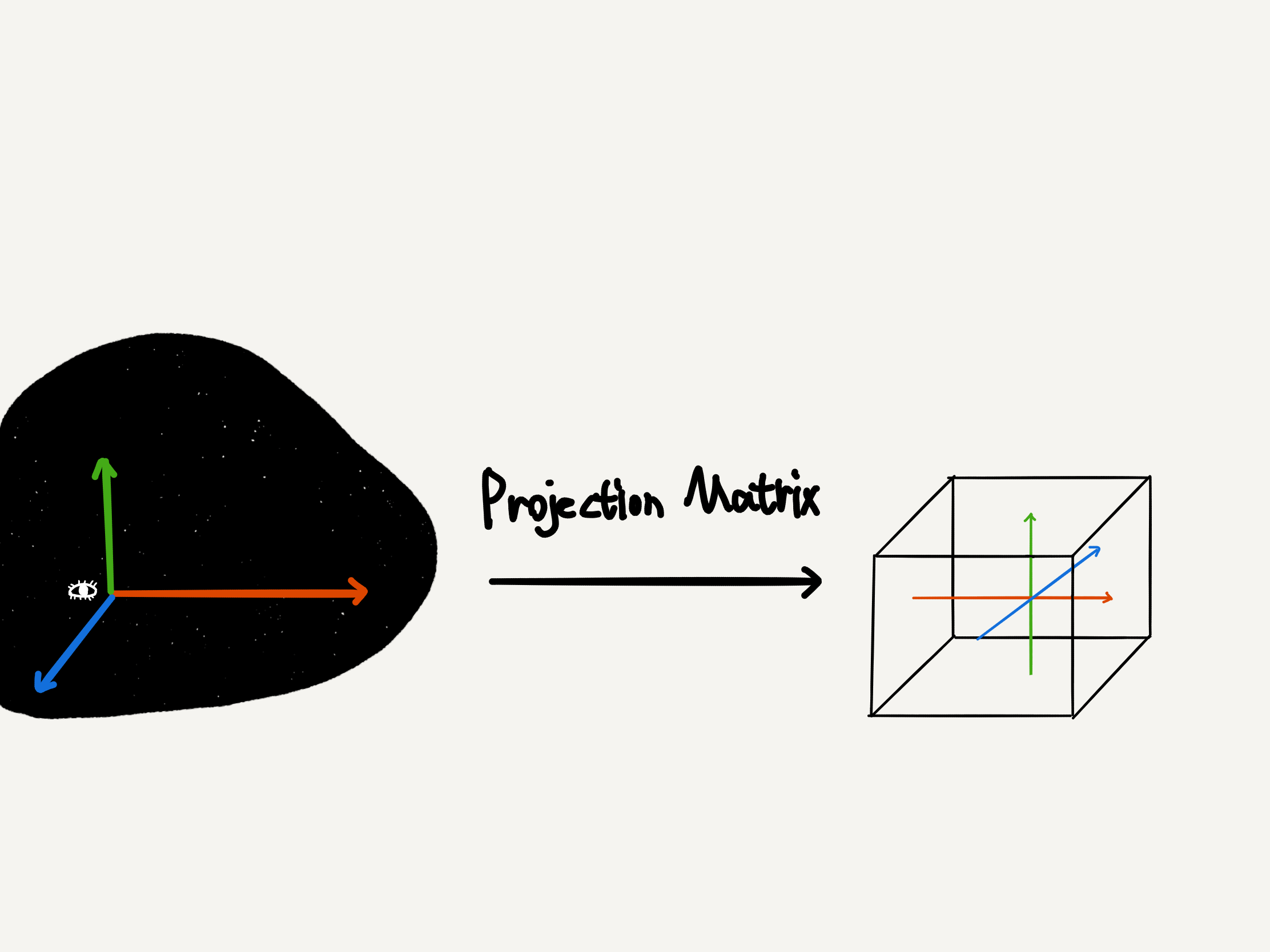
而投影矩阵的目的是为了把这样的一个坐标系映射到 NDC 空间中,即:
$$ \text{NDC} = \bold{P} \cdot \bold{v}_{view} $$
其中 $\bold{P}$ 为投影矩阵,$v_{view}$ 为 view space 坐标系下的顶点坐标。又因为 NDC 坐标系是一个范围为 $[-1, 1]^3$ 的立方体, 因此可以把投影矩阵的作用理解为把 view space 的某个子空间映射到一个 $[-1, 1]^3$ 的立方体里。
正交投影
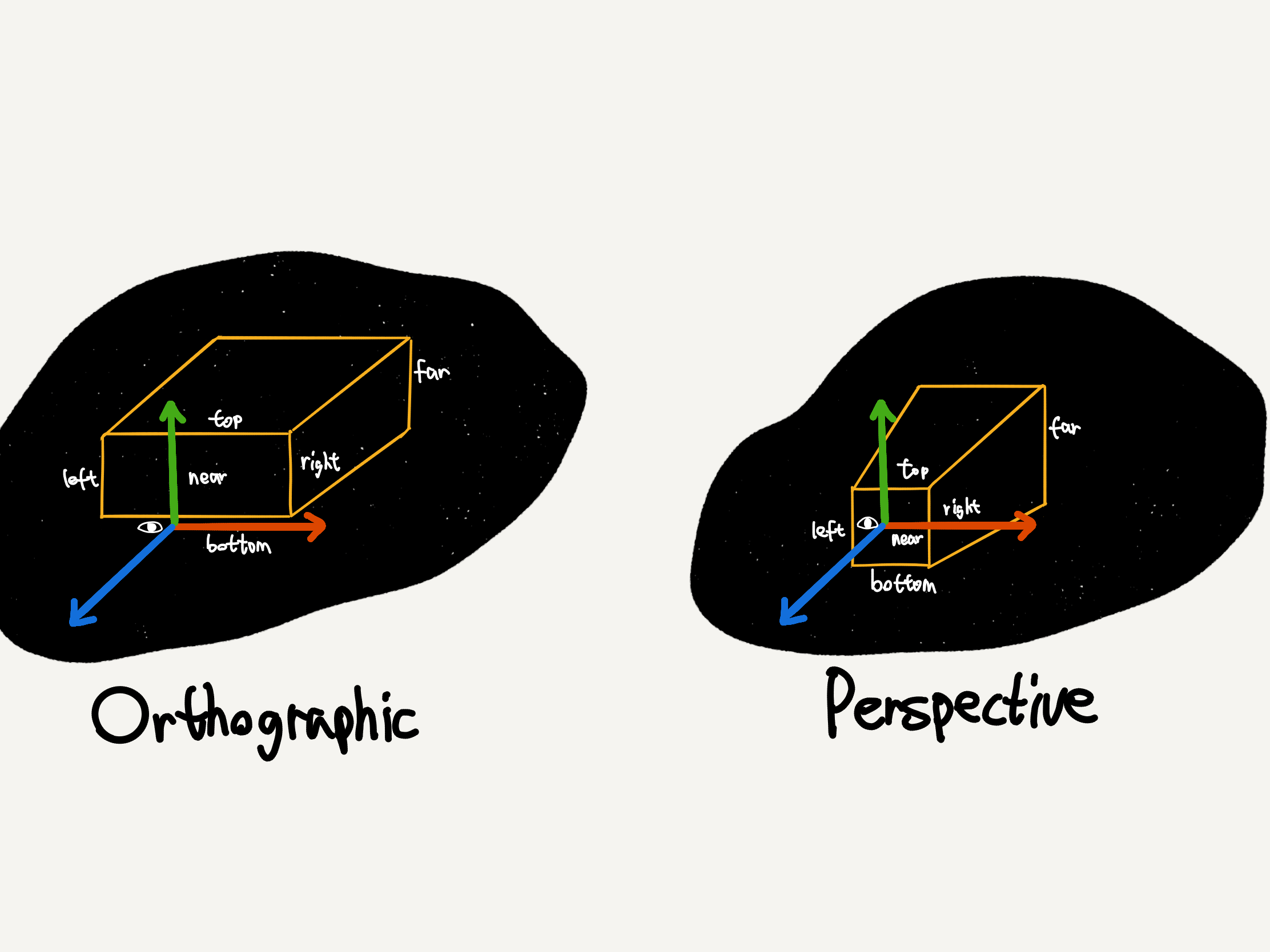
而对于正交投影,这个子空间就是 view space 里的一个立方体,我们用 6 个参数来定义个立方体的边界,分别是 top、bottom、left、right、near 和 far。注意,为了使使用者更加直观,参数 near 和 far 以 -z 轴为正。
要将该子空间立方体映射到 NDC 的 $[-1, 1]^3$ 立方体是非常简单的,类似把一个立方体模型变换成另一个立方体,即先缩放,再平移。
首先,根据子空间的定义,它的原点位于 $(\frac{right+left}{2}, \frac{top+bottom}{2}, -\frac{near+far}{2})$ ,用矩阵来表示这个立方体子空间话就是
$$ \bold{S} = \begin{bmatrix} \frac{right-left}{2} & 0 & 0 & \frac{right+left}{2} \\ 0 & \frac{top-bottom}{2} & 0 & \frac{top+bottom}{2} \\ 0 & 0 & -\frac{near-far}{2} & -\frac{near+far}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
先把该矩阵 $\bold{S}$ 缩放到 $[-1, 1]^3$,为此我们将一个缩放矩阵应用到 $\bold{S}$:
$$ \red{ \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & -\frac{2}{near-far} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} } \cdot \bold{S} $$
现在子空间的尺寸已经缩放到 2x2x2 了,而经过缩放矩阵后,原点也会进行缩放:
$$ \begin{pmatrix} \frac{2}{right-left} \cdot \frac{right+left}{2} \\ \frac{2}{top-bottom} \cdot \frac{top+bottom}{2} \\ -\frac{2}{near-far} \cdot -\frac{near+far}{2} \end{pmatrix} = \begin{pmatrix} \frac{right+left}{right-left} \\ \frac{top+bottom}{top-bottom} \\ \frac{near+far}{near-far} \end{pmatrix} $$
所以,为了把原点平移到 $(0,0,0)$,我们再应用一个平移矩阵:
$$ \red{ \begin{bmatrix} 1 & 0 & 0 & -\frac{right+left}{right-left} \\ 0 & 1 & 0 & -\frac{top+bottom}{top-bottom} \\ 0 & 0 & 1 & \frac{near+far}{near-far} \\ 0 & 0 & 0 & 1 \end{bmatrix} } \cdot \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & -\frac{2}{near-far} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \bold{S} $$
现在我们已经有了把 view space 下的立方体子空间映射到 $[-1,1]^3$ 的矩阵了。仔细观察上图,你会发现 view space 的 z 轴是指向屏幕外的,而 NDC 坐标系的 z 轴是指向屏幕内的,所以我们还需要反转 z 轴:
$$ \red{ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} } \cdot \begin{bmatrix} 1 & 0 & 0 & -\frac{right+left}{right-left} \\ 0 & 1 & 0 & -\frac{top+bottom}{top-bottom} \\ 0 & 0 & 1 & \frac{near+far}{near-far} \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2}{top-bottom} & 0 & 0 \\ 0 & 0 & -\frac{2}{near-far} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \bold{S} $$
最后,把左边的 3 个矩阵组合起来就是正交矩阵了:
$$ \begin{bmatrix} \frac{2}{right-left} & 0 & 0 & -\frac{right+left}{right-left} \\ 0 & \frac{2}{top-bottom} & 0 & -\frac{top+bottom}{top-bottom} \\ 0 & 0 & \frac{2}{near-far} & \frac{near+far}{near-far} \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
透视投影
透视投影也是一样的原理,只不过透视投影的子空间是 view space 内的一个四棱台,而不是立方体。
在立方体投影中,子空间的缩放在恒定的,而对于透视投影,这是不可行的,因为这样无法把一个四棱台装到 NDC 立方体内。 四棱台的特定是前面小,后面大,除此之外,和立方体类似。因此,为了能够把一个前小后大的四棱台“塞进”一个前后均等的立方体里,我们能不能对四棱台进行缩放时,作的是一种可变的缩放呢?
例如,对于靠前面的区域,我们缩放小一点,而对于靠后面的区域,我们缩放大一点,因此我们的缩放比例可以看做是和 z 相关的函数。
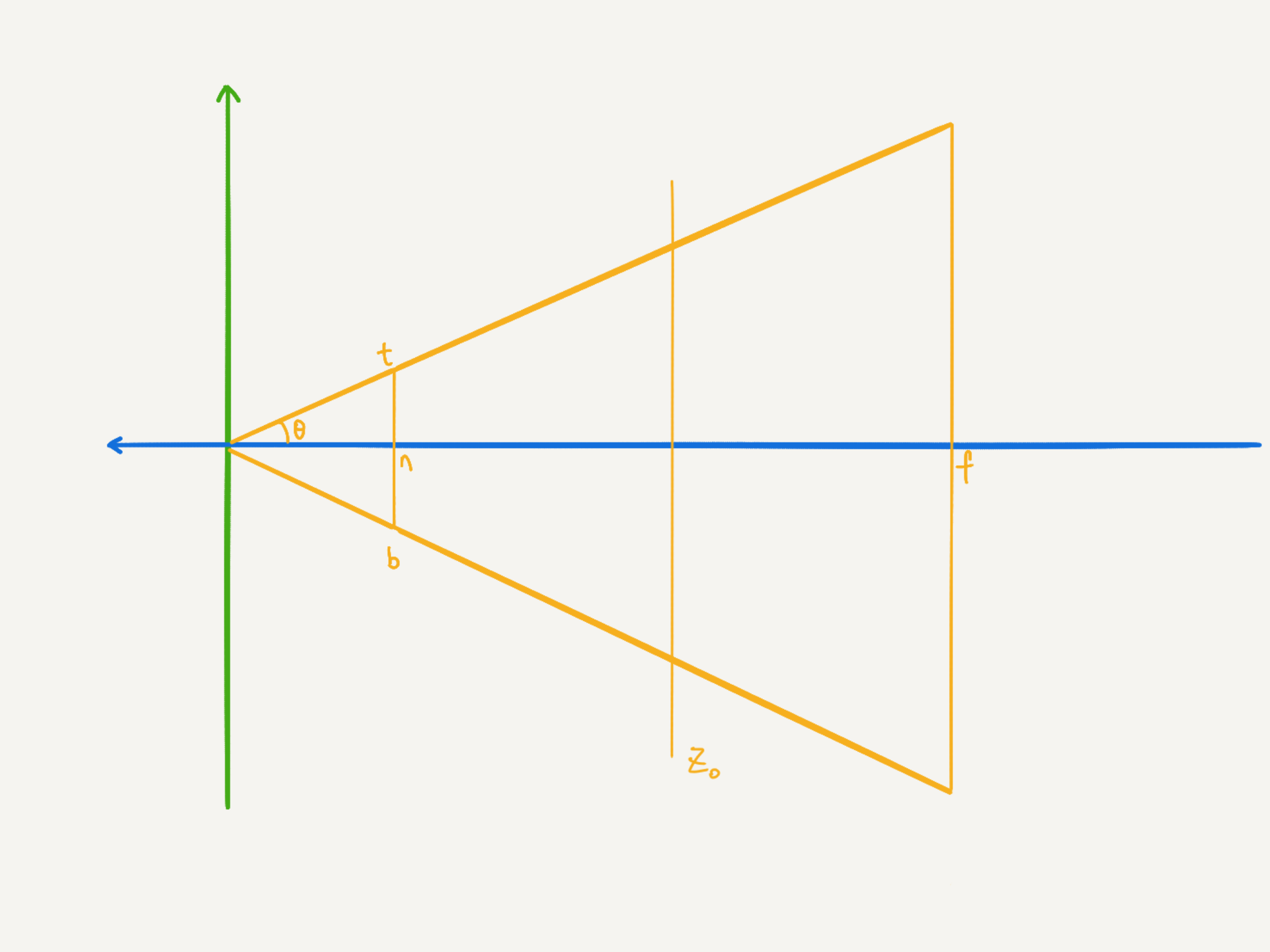
首先,我们需要定义这个四棱台,我们还是用之前的 6 个参数来定义。
且
- 对于近平面 $z = -near$,它在 x 轴的范围为 $[left, right]$,在 y 轴的范围为 $[bottom, top]$
- 对于远平面 $z = -far$,它的范围为近平面的 $\frac{far}{near}$ 倍
我们需要把它们的范围都缩放到 $[-1,1]$,所以
- 近平面在 x 轴上是 NDC 的 $\frac{right-left}{2}$ 倍,在 y 轴是 NDC 的 $\frac{top-bottom}{2}$ 倍,
- 而远平面则是近平面的 $\frac{far}{near}$ 倍,
- 对于那些在近平面和远平面之间的平面 $z=-z_0, z_0 \in (n, f)$ 来说,它们的倍数则为近平面的 $\frac{z_0}{near}$ 倍,即在 x 轴和 y 轴上分别为 $\frac{right-left}{2}\cdot\frac{z_0}{near}$ 和 $\frac{top-bottom}{2}\cdot\frac{z_0}{near}$。
因此,对于四棱台内的任一 z 平面 $z=z_0$ 来说,为了把它们映射为 NDC 立方体对应的 z 平面,我们可以得到 view space 的 Z 平面和 NDC 的 Z 平面上的点之间的关系为:
$$ \begin{matrix} x_{view} = x_{NDC} \cdot (\frac{right-left}{2}\cdot\frac{z_0}{near}) \\ y_{view} = y_{NDC} \cdot (\frac{top-bottom}{2}\cdot\frac{z_0}{near}) \end{matrix} $$
然后调整为这样的形式:
$$ \begin{matrix} x_{NDC} = \frac{\frac{2near}{right-left} \red{x_{view}}}{\red{z_0}} \\ y_{NDC} = \frac{\frac{2near}{top-bottom} \red{y_{view}}}{\red{z_0}} \end{matrix} $$
又因为 clip space 的坐标为
$$ \bold{v}_{clip} = \begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ ? & ? & ? & ? \\ ? & ? & ? & ? \\ m_{30} & m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix} x_{view} \\ y_{view} \\ z_{view} \\ 1 \end{bmatrix} $$
因此 $\bold{v}_{clip}$ 的 w 分量为 $w_{clip}=(m_{30} x_{view} + m_{31} y_{view} + m_{32} z_{view} + m_{33})$。又因为 NDC 坐标为 clip space 坐标除以 w 分量,所以 NDC 坐标为
$$ \bold{v}_{NDC} = \frac{\bold{v}_{clip}}{w_{clip}} = \frac{\bold{v}_{clip}}{(a x_{view} + b y_{view} + c z_{view} + d)} $$
对于 NDC 的 x 分量就是:
$$ x_{NDC} = \frac{x_{clip}}{w_{clip}} = \frac{m_{00} x_{view} + m_{01} y_{view} + m_{02} z_{view} + m_{03})}{(m_{30} x_{view} + m_{31} y_{view} + m_{32} z_{view} + m_{33})} $$
这就是投影矩阵必须要满足的形式。把它和之前的 $x_{NDC}$ 联立:
$$ \begin{matrix} x_{NDC} = & \frac{\frac{2near}{right-left} \red{x_{view}}}{\red{z_0}} \\ x_{NDC} = & \frac{m_{00} \red{x_{view}} + m_{01} y_{view} + m_{02} z_{view} + m_{03})}{(m_{30} x_{view} + m_{31} y_{view} + m_{32} \red{z_{view}} + m_{33})} \end{matrix} $$
可以得到 $m_{30} = 0, m_{31} = 0, m_{32} = -1, m_{33} = 0, m_{00} = \frac{2near}{right-left}$,注意,我们定义 $z_0$ 以 -z 轴为正,而 $z_{view}$ 以 z 轴为正,所以 $m_{32}=-1$。因此,可以得知透视投影矩阵:
$$ \bold{P} = \begin{bmatrix} \frac{2near}{right-left} & 0 & 0 & 0 \\ ? & ? & ? & ? \\ ? & ? & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} $$
对 y 轴应用同样的方法:
$$ \begin{matrix} y_{NDC} = & \frac{\frac{2near}{top-bottom} \red{y_{view}}}{\red{z_0}} \\ y_{NDC} = & \frac{m_{00} x_{view} + m_{01} \red{y_{view}} + m_{02} z_{view} + m_{03})}{(m_{30} x_{view} + m_{31} y_{view} + m_{32} \red{z_{view}} + m_{33})} \end{matrix} $$
得到 $m_{10} = 0, m_{11} = \frac{2near}{top-bottom}, m_{12} = 0, m_{13} = 0$:
$$ \bold{P} = \begin{bmatrix} \frac{2near}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2near}{top-bottom} & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} $$
至于 z 轴,因为 $m_{30} = 0, m_{31} = 0, m_{32} = -1, m_{33} = 0$ 了,所以 $z_{NDC}$ 只能是这样的形式:
$$ z_{NDC} = \frac{m_{20} x_{view} + m_{21} y_{view} + m_{22} z_{view} + m_{23}}{z_0} $$
又因为我们要把同一 z 平面的点映射之后,这些点的 $z_{NDC}$ 值也是一样的,所以 $z_{NDC}$ 与 $x_{view}$ 或 $y_{view}$ 无关,因此:
$$ z_{NDC} = \frac{m_{22} z_{view} + m_{23}}{z_0} $$
又因为 $z_{view} = -z_0$,所以:
$$ z_{NDC} = \frac{m_{22} (-z_0) + m_{23}}{z_0} = -m_{22} + \frac{m_{23}}{z_0} $$
这里可以看到,$z_0$ 和 $z_{NDC}$ 成反比,即 $z_0$ 越大,$z_{NDC}$ 的精度越小(为了把近处的精度分一点给远处,可以考虑对数深度)。我们需要把 $[near, far]$ 映射到 $[-1, 1]$,所以当 $z_0=near$ 时,$z_{NDC}=-1$,当 $z_0=far$ 时,$z_{NDC}=1$:
$$ \begin{matrix} -1 & = - m_{22} + \frac{m_{23}}{near} \\ 1 & = - m_{22} + \frac{m_{23}}{far} \end{matrix} $$
解得 $m_{22} = \frac{near+far}{near-far}, m_{23} = \frac{2far \cdot near}{near-far}$,所以透视投影矩阵为
$$ \bold{P} = \begin{bmatrix} \frac{2near}{right-left} & 0 & 0 & 0 \\ 0 & \frac{2near}{top-bottom} & 0 & 0 \\ 0 & 0 & \frac{near+far}{near-far} & \frac{2far \cdot near}{near-far} \\ 0 & 0 & -1 & 0 \end{bmatrix} $$
下面是一些值得思考的问题:
- 这是屏幕中心点位于近平面中心点的情况,对于 off center 的情况呢?
- 映射的精度又是多少?
总结
可以把投影矩阵理解成是一个“映射矩阵”,它的作用就是把一个三维空间上的点映射为另一个三维空间的点,其中,前一个三维空间是 view space 的一个子空间(对于正交投影,该子空间是立方体,对于透视投影,该子空间是四棱台),后一个三维空间是 $[-1,1]^3$ 的 NDC 空间。